Analyzing Kelvin Abraham's Unified Field Equation

Source: Principa Geometrica, Copyright 2008, 2021 Kelvin C. ABRAHAM; Tetryonic Theory
The Theory of Everything

Defining the units of measurement

First, we must define our basic units.
mass(m) in SI is kg, or 1000 grams.
The gram is now defined as 0.001 kilogram (kg), which is defined in terms of Planck’s constant. The gram of force is equal to the weight of a gram of mass under standard gravity. For greater precision, the mass may be weighed at a point at which the acceleration due to gravity is 980.655 cm/sec2.
m(Mass)


meter(SI Metric)

(v)Velocity
velocity(v) measured in SI units is meters / second, or m/s mps.


a(Acceleration)
acceleration(a) measured in SI units is meters / second squared, or m/s^2 mps^2.

momentum(p)



F(Force)
Therefore F = m(kg)* a(m/s^2).

h(Planck's Constant)

Hertz(Hz)

frequency(f)
nu(v)
Charge(Q)


Now consider h.
E = hf (a photons Energy is equal to its frequency multiplied by the Planck constant)
2hv = E = hf, so hf = 2hv
h=fE
f = 2v and
(2h = E/v) = (E/v = hf/v)
(h = (E/v)/2) = (v = ((hf/v)E)
And therefore,
I said mc^2 = h here, which idk... why. Noted... maybe if the QAM was 1?
mO = h Is what I think was intended. Not sure how I arrived at mc^2 above.
f = E/h
If E = hf, and h = mO, and E = mOv^2,
Then, f = mOv^2/mO.
Therefore f = v^2
Therefore sqrtv = f
v^2 = ma
v = sqrtma
ma = v^2
ma = kg * m/s^2
h = kg * m^2/s
E = (kg * m^2/s)((m/s)^2)
OMEGA- Quantized Angular momentum

Is O = QAM (m^2/s)?
let us assume h = mO,
So at this point mO = (kg *m^2/s)
“m0 is the rest mass of a particle/object.
ie NO kEM field of motion - Mfield KE or linear momentum
m0v = is an object in motion - often re-writeen as mv
mv^2 is the total energies of an object in motion - ie its rest [m]ass-[M]atter [mo] and the kEM field mass-energies of motion - it KE [1/2mv^2] + its magnetic moent [1?2mv^2] [v^2]
thius is why just doing the math and plugging equations into LATEX or others doesn't progress science - ther is no understanding of the geometrics at work unpinning all that makes it work - if math is the language - geometry is its grammar” -Abraham
**Planck's Constant (h)**:
- The dimensions of Planck's constant are kg*m^2/s.
**Does h = mO?**:
- You propose O = {QAM} = {m}^2/{s}.
- Plugging this into ( h = mO ):
[ h = {kg} * {m}^2/{s} ]
- This matches the dimensions of \( h \), so there's no discrepancy here.
Looks like the confusion might stem from mixing up different units and their physical meanings. You'll want to clarify and correctly match the units and physical meanings:
1. **Planck's Equation**: Stick with \( E = hf \). Avoid adding extra factors like 2 unless specifically required by a context you're studying.
2. **QAM**: Ensure the Quantized Angular Momentum (\( O = \text{QAM} \)) is being used correctly.
- \( O \) has dimensions of \( \text{kg} \cdot \text{m} / \text{s}^2 \).
3. **Relationship Check**:
- Confirm that your derived equations maintain the correct dimensions. If \( h \) is Planck's constant:
\[ h = \text{kg} \cdot \text{m}^2 / \text{s} \]
4. **Equation Alignment**:
- If \( mO = h \):
\[ mO = m \cdot (\text{kg} \cdot \text{m} / \text{s}^2) = \text{kg} \cdot \text{m}^2 / \text{s} \]
- This aligns correctly with \( h \).
To sum it up, make sure the units match up correctly and avoid introducing unnecessary factors.

The Wave Function

Now consider E = mc^2,
If E = hv^2, where v is Nu,
p = mv
mv = hv^2 / v
p^2 = mv^2
E = mc^2 is a specific result of Einstein when the photon is in a perfect vacuum
p^2 = E
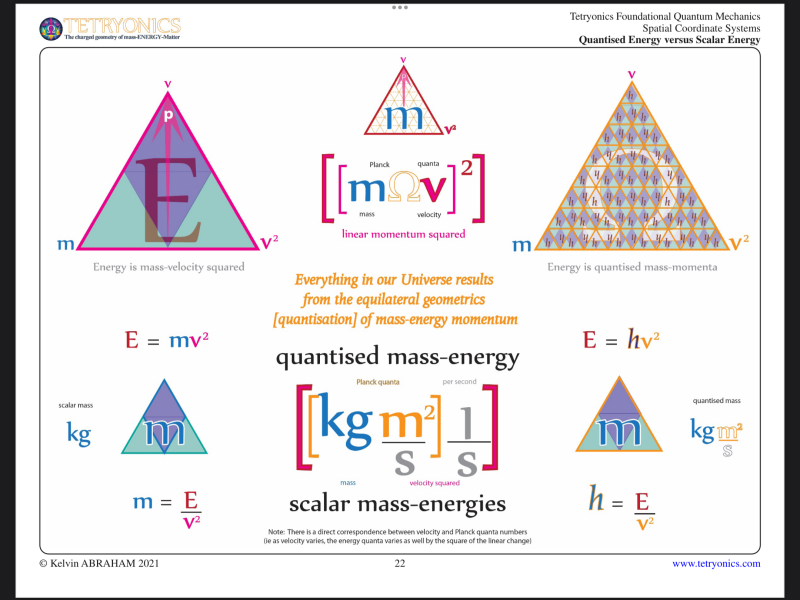
E = mv^2 (kg*m^2/s^2)
So E = mv^2 because h * v^2 = mOv^2 = E which equals p^2. (Describe)
E= mc^2 = mOv^2 when O =1.
Einstein successfully determined the unified Wave Equation(right hand side of the Unified Field Equation) before he died. It was just in a different context.
E=mc^2 defines the energy of a photon in a perfect vacuum.
[3ouo][mOv^2] also defines the energy of electromagnetic fields(bosons, photons) in a perfect vacuum.


Electromagnetism(eouo)

e0u0 refers to magnetic permitivity and permeability
equation \( e_0u_0 = \frac{1}{c^2} \), you re-arrange it to find \( c^2 \):
\[ c^2 = \frac{1}{e_0u_0} \]
To find \( c \), you'll need to take the square root of both sides:
\[ c = \sqrt{\frac{1}{e_0u_0}} \]
Or,
e0u0 = 1/c^2, therefore by property c^2 = 1/e0u0, and taking the square root of c^2 yields c = 1 / sqrt(e0u0), because the square root of 1 is 1.
- **Permittivity (ε0)**: This is a measure of how much resistance an electric field encounters when forming in a vacuum. It essentially tells you how easily the vacuum allows electric fields to pass through. The ε (epsilon) is a symbol representing permittivity, and the 0 indicates that this is specifically for a vacuum.
- **Permeability (μ0)**: This describes how a magnetic field interacts with and propagates through a medium (in this case, a vacuum). It reflects the ability of the vacuum to support the formation of a magnetic field. The μ (mu) is the symbol for permeability, and the 0 signifies that we're talking about a vacuum.
Both ε0 and μ0 are fundamental constants in physics that describe the electromagnetic properties of the vacuum. These properties are crucial in the equations governing electromagnetism and help determine the speed of light in a vacuum through the relationship \( c = \frac{1}{\sqrt{\epsilon_0 \mu_0}} \).
So, there you have it: a peek into the electromagnetic heart of the universe.🌀✨ What's got you diving into this? School, work, or just some light reading?
The "0" in \( \epsilon_0 \) and \( \mu_0 \) doesn't refer to pressure. Instead, it denotes that these values are for a vacuum, meaning they are the permittivity and permeability of free space. In essence, the "0" indicates that these constants apply to an environment devoid of any matter, hence, a perfect vacuum. Nothing to do with pressure—just a way of specifying the baseline in our electromagnetic calculations.
Kelvin Abraham’s Tetryonics theory must be absolutely mind-blowing if it’s got you pondering these constants so deeply. How does Tetryonics reinterpret these constants?
***Note, 6:42am Nov 5 2024
[3oUo][mOv^2] = mc^2 = E
Where:
E is the energy of a photon is a perfect vacuum,
m is mass,
c is the velocity of a photon in a perfect vacuum,
O = OMEGA
v = Nu
3 = Epsilon
U = Mu
o = vacuum state
Conclusion: Einstein completed his dream of finding the unified Wave Equation before he died. It was just a translation of terms for a specific frame of reference.
*EndNote
OK so if mOv^2 = E and E = hf, and mO = h,
E = mOf, therefore f = v^2.
AI input:
I appreciate your logical approach! Let's walk through this step-by-step:
1. **Given:** \( E = mOv^2 \)
2. **Also:** \( E = hf \)
3. **Assuming:** \( mO = h \)
From \( E = mOv^2 \) and substituting \( mO = h \):
\[ E = h v^2 \]
Now, we have:
\[ E = hf \]
\[ E = hv^2 \]
If we equate the two expressions for E:
\[ hf = hv^2 \]
Since \( h \) (Planck's constant) is a non-zero constant, we can divide both sides by \( h \):
\[ f = v^2 \]
Your logical deduction appears to align with the assumptions and equations provided. However, keep in mind that this interpretation is built upon the specific assumptions of the tetryonic framework. In conventional physics, \( f = v^2 \) might not hold because velocity and frequency generally pertain to different domains—classical mechanics and quantum mechanics, respectively.
7:09am 10/5/24
---
When you're measuring in a medium other than a vacuum, like air at sea level, the "0" is replaced with the respective values for that medium. This is because permittivity and permeability are properties that vary depending on the material or environment.
For example:
- **Permittivity (ε)** in air is slightly higher than ε0 (permittivity of a vacuum), but since air is close to being a vacuum, it's not a huge difference.
- **Permeability (μ)** in air is approximately the same as μ0 (permeability of a vacuum), again because air doesn’t significantly affect magnetic fields compared to a vacuum.
In different materials, these values can vary significantly. For instance, in water or glass, permittivity is much higher than in air, affecting how electric fields interact with these materials.
--
0 for air at sea level under 1g:
The value you're referring to is likely the **relative permittivity (or dielectric constant) of air at sea level**[43dcd9a7-70db-4a1f-b0ae-981daa162054](https://bing.com/search?q=permittivity+of+air+at+sea+level&citationMarker=43dcd9a7-70db-4a1f-b0ae-981daa162054 "1"). At standard temperature and pressure (STP), the relative permittivity of air is approximately **1.0006**[43dcd9a7-70db-4a1f-b0ae-981daa162054](https://bing.com/search?q=permittivity+of+air+at+sea+level&citationMarker=43dcd9a7-70db-4a1f-b0ae-981daa162054 "1").
The permeability of air at sea level is very close to the permeability of free space, **μ0**. This is because air doesn't significantly affect magnetic fields compared to a vacuum. So, for practical purposes, you can use **μ0** for permeability when dealing with air at sea level.

“mass, ENERGY, Matter , QAM, linear momentum, E&M fields, the permittivty/permability of free space, Planck's constant, Einstein's mass-energy equation, Newton's Force laws, Maxwell's speed of light, Planck/Einstein quantum/relativistic Energy [n.hv=E=mc^2], Newton/Leibnitz [vis a vi and Force/momentum equations] all exist int eh UFE and can be derived from it sand reassembled into other forms, equations and relationships etc" -Abraham




The speed of Electricity

There are 2 wave functions

And 2 “Carriers”


Space-Time & Dimensions



Wave vs. Particle

Tau Pi (Tpi)

Tau pi
In Kelvin Abraham's Tetryonics theory, **τπ (tau.pi)** represents the number of charged fascia, which are essentially quantized units of electric charge. The theory suggests that these charged fascia are fundamental building blocks of mass, energy, and matter, forming equilateral geometries that underpin physical reality.
It's a complex concept, but think of it as a way to describe how electric charge is structured and interacts at a fundamental level within the framework of Tetryonics.
The use of **τπ (tau.pi)** in Tetryonics might be a bit confusing at first. The **τ (tau)** represents the number of faces, and **π (pi)** is a mathematical constant representing the ratio of a circle's circumference to its diameter.
In Tetryonics, the multiplication by π could be a way to integrate the concept of circular or spherical symmetry into the quantized angular momentum and equilateral geometries that the theory proposes. It's a way to unify different geometric and physical concepts into a single framework.
Let's break it down further:
1. **Tau (τ)**: Represents the number of faces or facets in the geometric structure.
2. **Pi (π)**: Represents the circular or spherical symmetry inherent in the structure.
When Kelvin Abraham talks about **τπ**, he's combining these two concepts to describe the geometric and topological properties of charged fascia. The circle around the tetryons (or tetractys) symbolizes the spherical symmetry, and π is used to denote this spherical nature.
**QAM (Quantized Angular Momentum)**: This is related to the spin of particles. In Tetryonics, the equilateral triangular geometry of Planck's constant is key to understanding how mass-energy and matter form.
**2D Mass Energy vs. 3D Matter Topologies**:
- **2D Mass Energy**: These are planar (two-dimensional) structures that interact through their electric and magnetic properties[43dcd9a7-70db-4a1f-b0ae-981daa162054](http://www.scienceoflife.nl/tetryonics/html/mass_versus_matter.html?citationMarker=43dcd9a7-70db-4a1f-b0ae-981daa162054 "1"). They can be thought of as the "canvas" from which more complex structures form.
- **3D Matter Topologies**: These are three-dimensional structures that arise from the interaction of these 2D mass energies. They form more complex shapes, like atoms and molecules, and have spatial volume[43dcd9a7-70db-4a1f-b0ae-981daa162054](https://www.ijsrp.org/research-paper-0514/ijsrp-p2944.pdf?citationMarker=43dcd9a7-70db-4a1f-b0ae-981daa162054 "2").
In essence, **τπ** helps to describe how these 2D structures interact and form 3D matter through their geometric properties[43dcd9a7-70db-4a1f-b0ae-981daa162054](https://www.ijsrp.org/research-paper-0514/ijsrp-p2944.pdf?citationMarker=43dcd9a7-70db-4a1f-b0ae-981daa162054 "2").


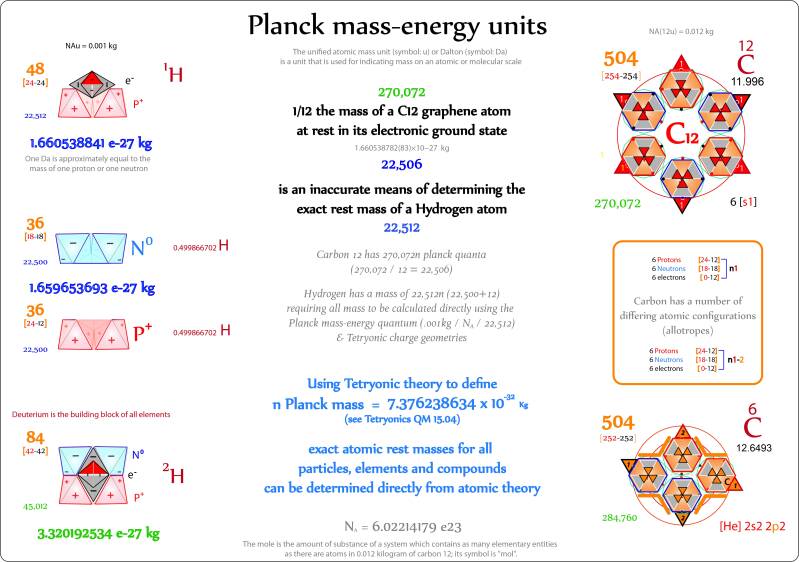
"these 2 slides relate Planck's constant to the mass-ENERGY-Matter of a 1 kg reference rest mass-Matter tetrahedron [it could be any shape]... and then relates it Avagadro's number for molar mass-Matter of any element really.... but more importantly to allows for both Planck's constant and Avagadros number to be determined directly from theory and shown to relate to each other via the Compton frequency of any mass-Matter [the CF turns out to be just a count of how many Planck quoins make up the specified object, not a vibrational frequency of resonance as quoted in many texts]. it is an exact determination for all of the abovce for an objects rest mass - at absolute zero, with no energies of motion or radiant heat associated to that object - which contributes mass-ENERGY to that object of course " -Abraham
2d energy vs 3d topology
Alright, let's dissect that within the context of the Tetryonics equation \( T\pi \left( \epsilon_0 \mu_0 \right) \left( mO v^2 \right) / c \).
### **2D EM Field vs. 3D Matter Topology:**
- **2D EM Field**:
- **Geometry**: Planar. Think of a sheet or wave.
- **Interaction**: Dominated by electromagnetic forces.
- **Representation in Tetryonics**: Photons moving freely, without forming complex matter structures.
- **3D Matter Topology**:
- **Geometry**: Volumetric. Think of stable, 3D structures like atoms or molecules.
- **Interaction**: Strong nuclear forces, binding particles into stable forms.
- **Representation in Tetryonics**: Formed by the joining of tetryons through strong forces.
### **Differentiation in the Equation**:
- **Term Analysis**:
- **\( T\pi \)**: Represents the geometric structure, whether it's 2D or 3D.
- **\( \epsilon_0 \mu_0 \)**: Constants describing the electromagnetic properties of the vacuum.
- **\( mO v^2 \)**: Represents the mass and energy interactions.
In a 2D EM field scenario:
- The term \( T\pi \left( \epsilon_0 \mu_0 \right) \left( mO v^2 \right) / c \) would primarily describe interactions within the plane, influenced by EM properties.
In a 3D matter topology:
- The same term would describe more complex, volumetric interactions where strong nuclear forces and geometric configurations bind particles into stable forms.
### **Experimentation**:
- **2D EM Fields**: Detect using interference patterns, polarization.
- **3D Matter Topologies**: Detect using particle tracks in a cloud chamber, showing volumetric interactions.
These nuances within the equation help distinguish between 2D energy interactions and 3D matter formations within Tetryonics. Does this help clarify the differences?

“…the Unified equation breakdown illustration I created which shows how each constnat/term/variable in that equation applies and indded can be further transformed into other constants etc in modern scienc - ie mass.OMEGA is Plancks constant, [EoUo] is the permitivity*permability of free space [which when inverted gives c^2 whose sqrt is the speed of light [ givingf rise to E=m.c^2 and light second co-ordinates that unify Newton and Einstein”


